NeXus #0005
The weekly supplement for extra goodies.

The weekly supplement for extra goodies.
Around the Web:
A Soft Murmur
Mix ambient sounds together to wash away distraction and help you focus or relax
Articles:
Particle Physicists Detect ‘Magic’ at the Large Hadron Collider | Quanta Magazine
The supercollider is now being used to explore quantum phenomena, including a “magic” form of quantum entanglement.

The Real Reason Zebras Were Never Domesticated Like Horses
Humans spent centuries trying to tame zebras—but nature made sure they’d always stay wild.

Scientists make breakthrough toward ‘recharging’ of aging tissues
“This approach has the potential to rejuvenate specific tissues affected by mitochondrial decline,” author Gaharwar told Newsweek.
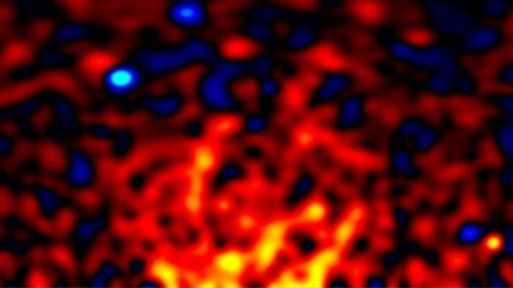
Scientists may have finally ‘seen’ dark matter for the 1st time
“This signifies a major development in astronomy and physics.”
Cats became our companions way later than you think
In true feline style, cats took their time in deciding when and where to join us on the sofa.

Scientists warn mountain climate change is accelerating faster than predicted, putting billions of people at risk
A major global review has revealed how climate change has impacted mountain regions over the last 40 years.

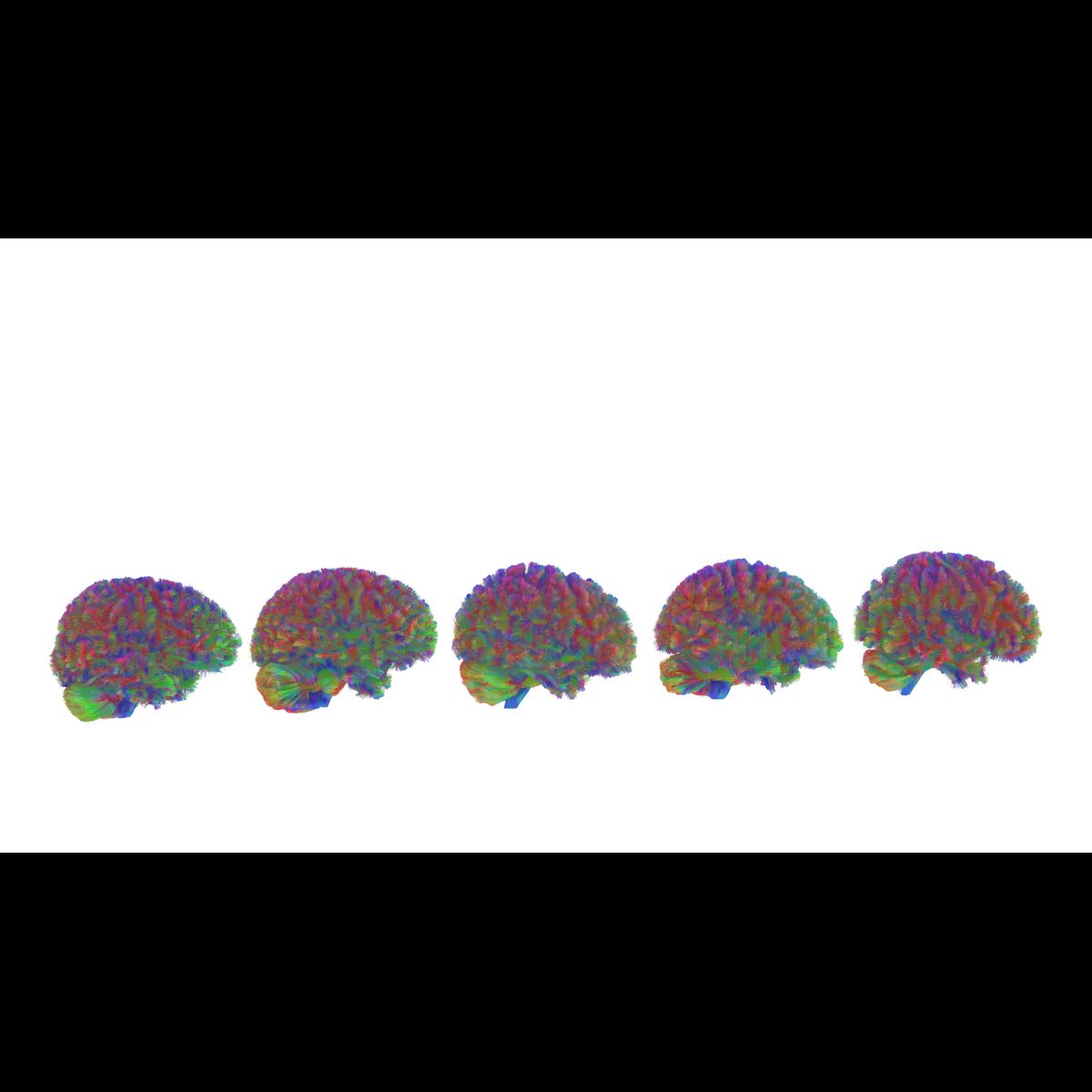
Scientists identify five ages of the human brain over a lifetime
Four major turning points around ages nine, 32, 66 and 83 create five broad eras of neural wiring over the average human lifespan.
The Land Beneath Antarctica’s Ice Might Be Full of Water - Eos
Seismic surveys hint at the extent of a potential groundwater system in the White Continent.

Ancient DNA Reveals Most Europeans Had Dark Skin Until Just 3,000 Years Ago
Pale skin didn’t dominate Europe until surprisingly recently.

The universe is a puzzle that fits together only one way
<p><em>Heraclitus famously argued that you can’t step into the same river twice. Here, philosopher JB Manchak argues that the whole universe is like that – and that such a universe has some interesting knock-on consequences. One being that although one can add more structure to a Heraclitus spacetime – by adding a big sign saying “here is the centre of the universe!” What one can’t do, Manchak argues, is reduce symmetries in a Heraclitus spacetime by adding such a sign. To illustrate the point, imagine the universe is a giant puzzle in which each event in space and time is a piece. In a non-Heraclitus universe, some pieces would be able to fit in several places. But in a Heraclitus universe, Manchak argues, there is exactly only one way to put the puzzle pieces of the universe together.</em></p><p> </p><p> </p><p>The ancient Greek philosopher <a href=“https://iep.utm.edu/heraclit/”>Heraclitus</a> is known for his theory of constant flux: “It is not possible to step twice into the same river.” It turns out that one can explore this idea within the context of Einstein’s general relativity. A four-dimensional “Heraclitus spacetime” is a model of the universe in which no two events have the same structure. This means that such models exhibit a radical type of spacetime asymmetry.</p><p>In what follows, I will first introduce the notion of Heraclitus spacetime within general relativity. To do this, a few basic definitions will be needed as well as a related discussion of spacetime symmetries. Next, I will highlight a curious result: if a model universe has the Heraclitus property, then its local structure completely fixes its global structure as well. In other words, bits of information encoded at each event allow one to piece together what the universe is like in its entirety (e.g. its shape). Finally, I will sketch a way in which the radical asymmetry present in a Heraclitus spacetime can be used to clarify a number of other topics in the philosophy of spacetime physics.</p><p>Let’s start with the three basic definitions: spacetimes, spacetime regions, and isomorphisms. A four-dimensional spacetime is a model of general relativity that represents a possible universe compatible with the theory. One can think of a spacetime as a collection of events with some additional structure that specifies how the events are related. Your birth is an event. So are any of your birthday parties. But your birthday is not an event and neither are you. </p><p>Although an event like your birthday party takes place in an extended space over an extended time, for our purposes “events” will be highly localized, point-like happenings. Experience seems to tell us that any event can be characterized by four numbers: one time coordinate <em>t</em> and three spatial coordinates <em>x</em>,<em>y</em>,<em>z</em>. Accordingly, the local structure of spacetime resembles a four-dimensional Cartesian coordinate system. Diagrams can help us “see” this spacetime structure. Consider a spacetime diagram of you stepping into a river twice.</p><p><img class=“leftAlone” title=”″ style=“display: block; margin-left: auto; margin-right: auto;” src=“assets/Uploads/_resampled/ResizedImageWzYwMCw1MTVd/IMAGE-1-copy.webp” alt=“IMAGE 1 copy” width=“600″ height=“515”></p><p>Following a long tradition, the time axis <em>t</em> is vertical with the up arrow pointing in the future direction. Two spatial dimensions <em>x</em> and <em>y</em> are also depicted with the <em>z</em> dimension suppressed. At any particular time t, you are located at a particular point in space, i.e. the <em>x-y</em> plane in the diagram. As time passes, these “you-points” create <a href=“articles/the-universe-is-unknowable-from-within-it-auid-3057”>a curve in spacetime</a>: the four-dimensional you depicted in the diagram. Similarly, at any particular time, the river is represented as a long strip in space. As time passes, these “river-strips” create the four-dimensional river shape depicted in the diagram. With the passing of time, you approach the river and then meet it at a single spacetime point. This is the “step 1” event. You then briefly move away from the river before returning to meet it a second time. This is the “step 2” event. After that, you move away from the river for good. </p><p>In the neighborhood of each step event, there is a region demarcated within a dotted line. For our purposes, a spacetime region is a connected area that counts as a model of general relativity in its own right. This means that if all events outside the dotted line surrounding step 1 were removed, the resulting spacetime structure would represent a possible universe compatible with the theory. The same point applies to the spacetime region surrounding step 2. </p><p>Next, we need a definition that captures when a pair of spacetimes (or spacetime regions) have the same structure. Recall that a spacetime is a collection of events with some additional structure that specifies how the events are related. An isomorphism between a pair of spacetimes is a map that (i) takes each event in one spacetime into exactly one event in the other spacetime and whose inverse does the same, and (ii) is such that both it and its inverse preserve all relevant structure. </p><p>An example isomorphism might help to illustrate this notion. Suppose that your two steps into the river are separated by a single<em> t</em> unit—say, one year. Suppose further that the spacetime regions surrounding the two steps are identical. In the diagram, this is represented by the fact that the colors and shapes of you and the river are duplicated exactly in both spacetime regions. Under these suppositions, the translation map that shifts each event (<em>t</em>, <em>x</em>, <em>y</em>, <em>z</em>) in the spacetime region surrounding step 1 up to the event (<em>t</em>+1, <em>x</em>, <em>y</em>, <em>z</em>) in the spacetime region surrounding step 2 is an isomorphism between these two spacetime regions. </p><p>Now that we have defined spacetimes, spacetime regions, and isomorphisms, we are ready to discuss symmetries. A global symmetry of a spacetime is an isomorphism from it to itself. Every spacetime has a trivial global symmetry: the identity map. This map is defined by taking any event in the spacetime into itself. </p><p>Virtually all spacetime models found in general relativity textbooks have other, non-trivial global symmetries as well. Consider, for example, the spacetime of special relativity which is called “Minkowski spacetime.” Minkowski spacetime is completely void of matter and is “flat” in the sense that there is no spacetime curvature whatsoever at any event. In the diagram below, this flatness is represented by the monotone color choice.</p><p><img class=“leftAlone” title=”″ style=“display: block; margin-left: auto; margin-right: auto;” src=“assets/Uploads/_resampled/ResizedImageWzYwMCw1MTVd/IMAGE-2-copy.webp” alt=“IMAGE 2 copy” width=“600″ height=“515”></p><p>Minkowski spacetime has many different types of global symmetries. Indeed, any event can be taken into any other via some translation symmetry. In the diagram, imagine shifting the entire spacetime some number of units to the right (along the <em>x</em>-axis) and then some number of units up (along the <em>t</em>-axis) until the event labeled “here-now” is mapped into the event labeled “there-then.” This is a translation symmetry which shows that the event here-now has the same structure as the event there-then. </p><p>Rotations are another type of global symmetry. In the diagram, imagine spinning the spacetime around the <em>t</em>-axis to some degree. This rotation does not map the event here-now into the event there-then, but remember: those are just labels, and all of the structure of Minkowski spacetime itself (which doesn’t come with labels) is preserved. </p><p>Reflections are global symmetries that are easy to define in standard coordinates. For example, a reflection across the <em>x</em>=0 plane maps each event (<em>t</em>, <em>x</em>, <em>y</em>, <em>z</em>) to the event (<em>t</em>, <em>-x</em>, <em>y</em>, <em>z</em>). Translation, rotation, and reflection symmetries should be very familiar to us since they are also found within the context of Euclidean space (which is flat like Minkowski spacetime). But Minkowski spacetime also has unusual “boost” symmetries that won’t be considered here.</p><p>A local symmetry of a spacetime is an isomorphism between a pair of its spacetime regions. Consider the spacetime regions surrounding the events here-now and there-then, which are demarcated with dotted lines. The global translation symmetry mentioned above that shifts the event here-now into the event there-then can be used to define a local symmetry from the spacetime region surrounding here-now to the spacetime region surrounding there-then. </p><p class=“article-plus-content--header” style=“text-align: center;”>___</p><p class=“article-plus-content--header” style=“text-align: center;”>If a spacetime has only trivial local symmetries, then there cannot be a (non-trivial) local symmetry taking one event into another: each event is different from every other.</p><p class=“article-plus-content--header” style=“text-align: center;”>___</p><p>Just as every spacetime has a trivial global symmetry (the identity map), every spacetime has an infinite number of trivial local symmetries in the following sense: Choose any one of the spacetime’s infinitely many spacetime regions. The identity map from this spacetime region to itself counts as a local symmetry of the spacetime. </p><p>With the notion of trivial local symmetries in hand, defining a Heraclitus spacetime is easy. This is just a spacetime in which all local symmetries are trivial. In other words, Heraclitus spacetimes exhibit radical asymmetry in the sense that they have the fewest possible local symmetries—only the trivial ones. How is this connected to the idea that you can’t step into the same river twice? If a spacetime has only trivial local symmetries, then there cannot be a (non-trivial) local symmetry taking one event into another: each event is different from every other. So the river stepping example fails to be a Heraclitus spacetime since the distinct events step 1 and step 2 have spacetime regions surrounding them (those demarcated by the dotted lines in the diagram) which are related by local symmetry taking step 1 into step 2. </p><p>It is a bit tricky to find concrete examples of Heraclitus spacetimes. Models of general relativity usually have many types of non-trivial symmetries (local and global) to make them simple enough to construct and study. And yet there are reasons to think that Heraclitus spacetimes not only exist but that, among all models of general relativity, they are generic in some sense. This is difficult to prove in general, however (see <a href=“https://www.jstor.org/stable/1971195”>Sunada 1985</a> and <a href=“https://arxiv.org/abs/1403.0182″>Mounoud 2015</a> for some related partial results). </p><p>There do exist simple examples of Heraclitus spacetimes and they can be easily visualized—especially in two dimensions. Start with a two-dimensional version of Minkowski spacetime. Then smoothly distort the flat spacetime structure so as to introduce two types of spacetime curvature—call them <em>Q</em> and <em>R</em>—that are carefully chosen to have the following property: although distinct events can share either the same <em>Q</em> curvature structure or the same <em>R</em> curvature structure, they can’t share both. Since any isomorphisms between any spacetime regions must preserve the curvature structure, it follows that the spacetime must be Heraclitus. </p><p><img class=“leftAlone” title=”″ style=“display: block; margin-left: auto; margin-right: auto;” src=“assets/Uploads/_resampled/ResizedImageWzYwMCw0Njdd/IMAGE-3-copy.webp” alt=“IMAGE 3 copy” width=“600″ height=“467”></p><p>In the diagram above, the color hue (a value on the red to violet continuum) represents curvature Q and the color shade (a value on the light to dark to continuum) represents curvature R. We see that no distinct events have both the same color hue and the same color shade. As before, you and a river are depicted along with the events step 1 and step 2 and their surrounding spacetime regions. But now there can be no local symmetry taking the step 1 into step 2 since these events have different curvature structures. The same is true for any distinct events. So, the spacetime is Heraclitus. </p><p>The radical asymmetry present in a Heraclitus spacetime allows one to show a curious result: if a model universe is Heraclitus, then its local structure completely fixes its global structure as well (e.g. its shape). Here’s a way to make this claim precise. Start with an arbitrary spacetime and consider any collection of overlapping spacetime regions that “cover” the entire spacetime. One can think of these spacetime regions as pieces to a giant puzzle—the original spacetime. Now we can play a game: if I give you all of the pieces but don’t tell you which spacetime they came from, can you “glue” them together in exactly one way to figure out the puzzle?</p><p><img class=“leftAlone” title=”″ style=“display: block; margin-left: auto; margin-right: auto;” src=“assets/Uploads/_resampled/ResizedImageWzYwMCw1OF0/IMAGE-4-copy.webp” alt=“IMAGE 4 copy” width=“600″ height=“58”></p><p>If the spacetime has non-trivial local symmetries, this may not be possible. Imagine the pieces in the first river stepping example are all the same size and sufficiently small (see diagram above). Because there are many duplicate pieces, you have a great deal of freedom in how to glue them back together. Of course, one solution recovers the original spacetime. To see another, just take the first solution and back up one step by removing a single piece located to the left of you and the river to make a “hole” in the spacetime (see diagram below). You can now glue this piece to a region just below the hole to get a second solution (complete overlap with other pieces is permitted). </p><p><img class=“leftAlone” title=”″ style=“display: block; margin-left: auto; margin-right: auto;” src=“assets/Uploads/_resampled/ResizedImageWzYwMCw0MTBd/IMAGE-5-copy.webp” alt=“IMAGE 5 copy” width=“600″ height=“410”></p><p>Now notice that if we play the game and the original spacetime is Heraclitus, then it doesn’t matter how small the pieces are—you are always able to figure out the puzzle. To see this, consider a collection of small pieces from the second river stepping example (see diagram below). </p><p><img class=“leftAlone” title=”″ style=“display: block; margin-left: auto; margin-right: auto;” src=“assets/Uploads/_resampled/ResizedImageWzYwMCw1N10/IMAGE-6-copy.webp” alt=“IMAGE 6 copy” width=“600″ height=“57”></p><p>The unique color properties of each piece radically constrain your gluing method; indeed, there is only one solution. This is because any overlapping pieces can be glued together in only one way if their color properties are to match up. So piece by piece, you are forced to reconstruct the original spacetime. Suppose you tried to obtain a second solution by removing a piece like you did in the first river stepping example (see diagram below). In order to get the color properties to match up, you would then find that the piece must be replaced exactly where it came from. </p><p><img class=“leftAlone” title=”″ style=“display: block; margin-left: auto; margin-right: auto;” src=“assets/Uploads/_resampled/ResizedImageWzYwMCwzNzhd/IMAGE-7-copy.webp” alt=“IMAGE 7 copy” width=“600″ height=“378”></p><p>The radical asymmetry present in a Heraclitus spacetime can be used to clarify a number of other topics in the philosophy of spacetime physics. For example, consider a widely held dogma: the symmetries of a spacetime are a good guide to its amount of structure. It is not always clear what philosophers mean by “structure” but an example below will help to illustrate the notion. The symmetry-structure dogma has been expressed in a variety of ways. For example, <a href=“https://mitpress.mit.edu/9780262550215/world-enough-and-space-time/”>John Earman (1989) writes</a> “As the space-time structure becomes richer, the symmetries become narrower,” and <a href=“https://global.oup.com/academic/product/physics-structure-and-reality-9780192894106?cc=gb&lang=en&”>Jill North (2021) writes</a> that one of the litmus tests for the presence of more structure is that the “associated group of structure-preserving transformations becomes narrower.” </p><p>Many natural ways of making the dogma precise turn out to be false given the existence of Heraclitus spacetimes (Manchak and Barrett 2023). To see this, first note that a simple way to add “structure” to a spacetime is to include a privileged curve in the model which represents <a href=“video/the-centre-of-the-universe”>“the center of the universe”</a> (cf. <a href=“https://mitpress.mit.edu/9780262550215/world-enough-and-space-time/”>Earman 1989</a>). Because of this extra structure, any global or local symmetries must preserve not just the background spacetime structure but also the privileged curve as well. One can verify that for many textbook examples, the effect of this extra structure is a narrowing of symmetries in accordance with the dogma. As we have seen, spatial translations are global symmetries of Minkowski spacetime. But they are <em>not</em> global symmetries of the pair consisting of Minkowski spacetime and the privileged curve: a spatial translation shifting the center of the universe three feet to the right does not map the center of the universe into itself (see diagram below). So the symmetry-structure dogma holds in this case—adding structure decreases the symmetries.</p><p><img class=“leftAlone” title=”″ style=“display: block; margin-left: auto; margin-right: auto;” src=“assets/Uploads/_resampled/ResizedImageWzYwMCw1MTVd/IMAGE-8-copy.webp” alt=“IMAGE 8 copy” width=“600″ height=“515”></p><p>Now consider any Heraclitus spacetime. Adding extra structure of any kind—including a privileged curve representing the center of the universe—does not result in narrowing symmetries. Why? Since Heraclitus spacetimes already have as few symmetries as possible, they cannot be decreased in any way. But although symmetries have reached a minimum, one can still add “structure” in the form of a privileged curve representing the center of the universe (see diagram below). So we have a counterexample to many precise formulations of the symmetry-structure dogma.</p><p><img class=“leftAlone” title=”″ style=“display: block; margin-left: auto; margin-right: auto;” src=“assets/Uploads/_resampled/ResizedImageWzYwMCw0Njdd/IMAGE-9-copy.webp” alt=“IMAGE 9 copy” width=“600″ height=“467”></p><p>Heraclitus spacetimes serve useful in exploring a number of other topics as well. Some examples include philosophical debates concerning “privileged coordinates” (<a href=“https://link.springer.com/article/10.1007/s10992-024-09773-4”>Barrett and Manchak 2024</a>), “cosmic underdetermination” (<a href=“https://link.springer.com/article/10.1007/s10992-024-09773-4”>Manchak and Barrett 2024</a>), and “determinism” (Halvorson et al. 2025). But there are also many open questions concerning Heraclitus spacetimes (these questions are listed in the papers just cited). What else can we learn by exploring radical asymmetry within the context of general relativity? </p>

How did the first words originate – possibly some 135,000 years ago?
The first words may have emerged 135,000 years ago.

How far back in time can the naked eye see?
Every observation out into deep space is also a look back in time.

What if a Tiny Black Hole Shot Through Your Body? A Physicist Did The Math
If you’ve ever wondered what would actually happen if a microscopic black hole tunneled straight through your body, answers have finally arrived.
A Cell So Minimal That It Challenges Definitions of Life | Quanta Magazine
The newly described microbe represents a world of parasitic, intercellular biodiversity only beginning to be revealed by genome sequencing.

Trailers:
Photos:





🔴
Nexus is a weekly selection of content elsewhere shared by their creators and hereby suggested by me. Please give the original authors their due recognition by supporting their work.




















